Array Operations
Overview
The array-operations system contains a collection of functions and
macros for manipulating Common Lisp arrays and performing numerical
calculations with them.
Array-operations is a ‘generic’ way of operating on array like data
structures. Several aops functions have been implemented for
data-frame. For those that haven’t, you can transform arrays to
data frames using the df:matrix-df function, and a data-frame to an
array using df:as-array. This make it convenient to work with the
data sets using either system.
Quick look
Arrays can be created with numbers from a statistical distribution:
(rand '(2 2)) ; => #2A((0.62944734 0.2709539) (0.81158376 0.6700171))
in linear ranges:
(linspace 1 10 7) ; => #(1 5/2 4 11/2 7 17/2 10)
or generated using a function, optionally given index position
(generate #'identity '(2 3) :position) ; => #2A((0 1 2) (3 4 5))
They can also be transformed and manipulated:
(defparameter A #2A((1 2)
(3 4)))
(defparameter B #2A((2 3)
(4 5)))
;; split along any dimension
(split A 1) ; => #(#(1 2) #(3 4))
;; stack along any dimension
(stack 1 A B) ; => #2A((1 2 2 3)
; (3 4 4 5))
;; element-wise function map
(each #'+ #(0 1 2) #(2 3 5)) ; => #(2 4 7)
;; element-wise expressions
(vectorize (A B) (* A (sqrt B))) ; => #2A((1.4142135 3.4641016)
; (6.0 8.944272))
;; index operations e.g. matrix-matrix multiply:
(each-index (i j)
(sum-index k
(* (aref A i k) (aref B k j)))) ; => #2A((10 13)
; (22 29))
Array shorthand
The library defines the following short function names that are synonyms for Common Lisp operations:
| array-operations | Common Lisp |
|---|---|
| size | array-total-size |
| rank | array-rank |
| dim | array-dimension |
| dims | array-dimensions |
| nrow | number of rows in matrix |
| ncol | number of columns in matrix |
The array-operations package has the nickname aops, so you can use,
for example, (aops:size my-array) without use‘ing the package.
Displaced arrays
According to the Common Lisp specification, a displaced array is:
An array which has no storage of its own, but which is instead indirected to the storage of another array, called its target, at a specified offset, in such a way that any attempt to access the displaced array implicitly references the target array.
Displaced arrays are one of the niftiest features of Common Lisp. When an array is displaced to another array, it shares structure with (part of) that array. The two arrays do not need to have the same dimensions, in fact, the dimensions do not be related at all as long as the displaced array fits inside the original one. The row-major index of the former in the latter is called the offset of the displacement.
displace
Displaced arrays are usually constructed using make-array, but this
library also provides displace for that purpose:
(defparameter *a* #2A((1 2 3)
(4 5 6)))
(aops:displace *a* 2 1) ; => #(2 3)
Here’s an example of using displace to implement a sliding window over some set of values, say perhaps a time-series of stock prices:
(defparameter stocks (aops:linspace 1 100 100))
(loop for i from 0 to (- (length stocks) 20)
do (format t "~A~%" (aops:displace stocks 20 i)))
;#(1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20)
;#(2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21)
;#(3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22)
flatten
flatten displaces to a row-major array:
(aops:flatten *a*) ; => #(1 2 3 4 5 6)
split
The real fun starts with split, which splits off sub-arrays nested
within a given axis:
(aops:split *a* 1) ; => #(#(1 2 3) #(4 5 6))
(defparameter *b* #3A(((0 1) (2 3))
((4 5) (6 7))))
(aops:split *b* 0) ; => #3A(((0 1) (2 3)) ((4 5) (6 7)))
(aops:split *b* 1) ; => #(#2A((0 1) (2 3)) #2A((4 5) (6 7)))
(aops:split *b* 2) ; => #2A((#(0 1) #(2 3)) (#(4 5) #(6 7)))
(aops:split *b* 3) ; => #3A(((0 1) (2 3)) ((4 5) (6 7)))
Note how splitting at 0 and the rank of the array returns the array
itself.
sub
Now consider sub, which returns a specific array, composed of the
elements that would start with given subscripts:
(aops:sub *b* 0) ; => #2A((0 1)
; (2 3))
(aops:sub *b* 0 1) ; => #(2 3)
(aops:sub *b* 0 1 0) ; => 2
In the case of vectors, sub works like aref:
(aops:sub #(1 2 3 4 5) 1) ; => 2
There is also a (setf sub) function.
partition
partition returns a consecutive chunk of an array separated along its
first subscript:
(aops:partition #2A((0 1)
(2 3)
(4 5)
(6 7)
(8 9))
1 3) ; => #2A((2 3)
; (4 5))
and also has a (setf partition) pair.
combine
combine is the opposite of split:
(aops:combine #(#(0 1) #(2 3))) ; => #2A((0 1)
; (2 3))
subvec
subvec returns a displaced subvector:
(aops:subvec #(0 1 2 3 4) 2 4) ; => #(2 3)
There is also a (setf subvec) function, which is like (setf subseq)
except for demanding matching lengths.
reshape
Finally, reshape can be used to displace arrays into a different
shape:
(aops:reshape #2A((1 2 3)
(4 5 6)) '(3 2))
; => #2A((1 2)
; (3 4)
; (5 6))
You can use t for one of the dimensions, to be filled in
automatically:
(aops:reshape *b* '(1 t)) ; => #2A((0 1 2 3 4 5 6 7))
reshape-col and reshape-row reshape your array into a column or row
matrix, respectively:
(defparameter *a* #2A((0 1)
(2 3)
(4 5)))
(aops:reshape-row *a*) ;=> #2A((0 1 2 3 4 5))
(aops:reshape-col *a*) ;=> #2A((0) (1) (2) (3) (4) (5))
Specifying dimensions
Functions in the library accept the following in place of dimensions:
- a list of dimensions (as for
make-array), - a positive integer, which is used as a single-element list,
- another array, the dimensions of which are used.
The last one allows you to specify dimensions with other arrays. For
example, to reshape an array a1 to look like a2, you can use
(aops:reshape a1 a2)
instead of the longer form
(aops:reshape a1 (aops:dims a2))
Creation & transformation
Use the functions in this section to create commonly used arrays
types. When the resulting element type cannot be inferred from an
existing array or vector, you can pass the element type as an optional
argument. The default is elements of type T.
Element traversal order of these functions is unspecified. The reason for this is that the library may use parallel code in the future, so it is unsafe to rely on a particular element traversal order.
The following functions all make a new array, taking the dimensions as
input. There are also versions ending in ! which do not make a
new array, but take an array as first argument, which is modified and
returned.
| Function | Description |
|---|---|
| zeros | Filled with zeros |
| ones | Filled with ones |
| rand | Filled with uniformly distributed random numbers between 0 and 1 |
| randn | Normally distributed with mean 0 and standard deviation 1 |
| linspace | Evenly spaced numbers in given range |
For example:
(aops:zeros 3)
; => #(0 0 0)
(aops:zeros 3 'double-float)
; => #(0.0d0 0.0d0 0.0d0)
(aops:rand '(2 2))
; => #2A((0.6686077 0.59425664)
; (0.7987722 0.6930506))
(aops:rand '(2 2) 'single-float)
; => #2A((0.39332366 0.5557821)
; (0.48831415 0.10924244))
(let ((a (make-array '(2 2) :element-type 'double-float)))
;; Modify array A, filling with random numbers
;; element type is taken from existing array
(aops:rand! a))
; => #2A((0.6324615478515625d0 0.4636608362197876d0)
; (0.4145939350128174d0 0.5124958753585815d0))
(linspace 0 4 5) ;=> #(0 1 2 3 4)
(linspace 1 3 5) ;=> #(0 1/2 1 3/2 2)
(linspace 1 3 5 'double-float) ;=> #(1.0d0 1.5d0 2.0d0 2.5d0 3.0d0)
(linspace 0 4d0 3) ;=> #(0.0d0 2.0d0 4.0d0)
generate
generate (and generate*) allow you to generate arrays using
functions. The function signatures are:
generate* (element-type function dimensions &optional arguments)
generate (function dimensions &optional arguments)
Where arguments are passed to function. Possible arguments are:
- no arguments, when ARGUMENTS is nil
- the position (= row major index), when ARGUMENTS is :POSITION
- a list of subscripts, when ARGUMENTS is :SUBSCRIPTS
- both when ARGUMENTS is :POSITION-AND-SUBSCRIPTS
(aops:generate (lambda () (random 10)) 3) ; => #(6 9 5)
(aops:generate #'identity '(2 3) :position) ; => #2A((0 1 2)
; (3 4 5))
(aops:generate #'identity '(2 2) :subscripts)
; => #2A(((0 0) (0 1))
; ((1 0) (1 1)))
(aops:generate #'cons '(2 2) :position-and-subscripts)
; => #2A(((0 0 0) (1 0 1))
; ((2 1 0) (3 1 1)))
permute
permute can permute subscripts (you can also invert, complement, and
complete permutations, look at the docstring and the unit tests).
Transposing is a special case of permute:
(defparameter *a* #2A((1 2 3)
(4 5 6)))
(aops:permute '(0 1) *a*) ; => #2A((1 2 3)
; (4 5 6))
(aops:permute '(1 0) *a*) ; => #2A((1 4)
; (2 5)
; (3 6))
each
each applies a function to its one dimensional array arguments
elementwise. It essentially is an element-wise function map on each of
the vectors:
(aops:each #'+ #(0 1 2)
#(2 3 5)
#(1 1 1)
; => #(3 5 8)
vectorize
vectorize is a macro which performs elementwise operations
(defparameter a #(1 2 3 4))
(aops:vectorize (a) (* 2 a)) ; => #(2 4 6 8)
(defparameter b #(2 3 4 5))
(aops:vectorize (a b) (* a (sin b)))
; => #(0.9092974 0.28224 -2.2704074 -3.8356972)
There is also a version vectorize* which takes a type argument for the
resulting array, and a version vectorize! which sets elements in a
given array.
margin
The semantics of margin are more difficult to explain, so perhaps an
example will be more useful. Suppose that you want to calculate column
sums in a matrix. You could permute (transpose) the matrix, split
its sub-arrays at rank one (so you get a vector for each row), and apply
the function that calculates the sum. margin automates that for you:
(aops:margin (lambda (column)
(reduce #'+ column))
#2A((0 1)
(2 3)
(5 7)) 0) ; => #(7 11)
But the function is more general than this: the arguments inner and
outer allow arbitrary permutations before splitting.
recycle
Finally, recycle allows you to reuse the elements of the first argument, object, to create new arrays by extending the dimensions. The :outer keyword repeats the original object and :inner keyword argument repeats the elements of object. When both :inner and :outer are nil, object is returned as is. Non-array objects are intepreted as rank 0 arrays, following the usual semantics.
(aops:recycle #(2 3) :inner 2 :outer 4)
; => #3A(((2 2) (3 3))
((2 2) (3 3))
((2 2) (3 3))
((2 2) (3 3)))
Three dimensional arrays can be tough to get your head around. In the example above, :outer asks for 4 2-element vectors, composed of repeating the elements of object twice, i.e. repeat ‘2’ twice and repeat ‘3’ twice. Compare this with :inner as 3:
(aops:recycle #(2 3) :inner 3 :outer 4)
; #3A(((2 2 2) (3 3 3))
((2 2 2) (3 3 3))
((2 2 2) (3 3 3))
((2 2 2) (3 3 3)))
The most common use case for recycle is to ‘stretch’ a vector so that it can be an operand for an array of compatible dimensions. In Python, this would be known as ‘broadcasting’. See the Numpy broadcasting basics for other use cases.
For example, suppose we wish to multiply array a, a size 4x3 with vector b of size 3, as in the figure below:
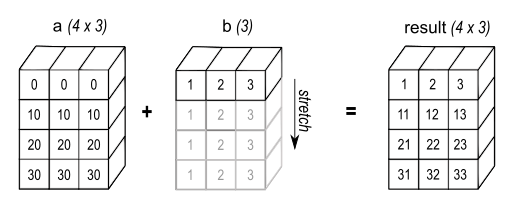
We can do that by recycling array b like this:
(recycle #(1 2 3) :outer 4)
;#2A((1 2 3)
; (1 2 3)
; (1 2 3)
; (1 2 3))
In a similar manner, the figure below (also from the Numpy page) shows how we might stretch a vector horizontally to create an array compatible with the one created above.
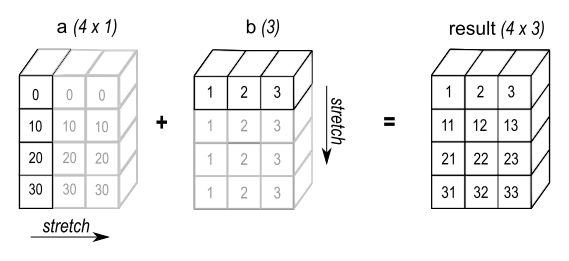
To create that array from a vector, use the :inner keyword:
(recycle #(0 10 20 30) :inner 3)
;#2A((0 0 0)
; (10 10 10)
; (20 20 20)
; (30 30 30))
turn
turn rotates an array by a specified number of clockwise 90° rotations. The axis of rotation is specified by RANK-1 (defaulting to 0) and RANK-2 (defaulting to 1). In the first example, we’ll rotate by 90°:
(defparameter array-1 #2A((1 0 0)
(2 0 0)
(3 0 0)))
(aops:turn array-1 1)
;; #2A((3 2 1)
;; (0 0 0)
;; (0 0 0))
and if we rotate it twice (180°):
(aops:turn array-1 2)
;; #2A((0 0 3)
;; (0 0 2)
;; (0 0 1))
finally, rotate it three times (270°):
(aops:turn array-1 3)
;; #2A((0 0 0)
;; (0 0 0)
;; (1 2 3))
map-array
map-array maps a function over the elements of an array.
(aops:map-array #2A((1.7 2.1 4.3 5.4)
(0.3 0.4 0.5 0.6))
#'log)
; #2A(( 0.53062826 0.7419373 1.4586151 1.686399)
; (-1.2039728 -0.9162907 -0.6931472 -0.5108256))
outer
outer is generalized outer product of arrays using a provided function.
Lambda list: (function &rest arrays)
The resulting array has the concatenated dimensions of arrays
The examples below return the outer product of vectors or arrays. This is the outer product you get in most linear algebra packages.
(defparameter a #(2 3 5))
(defparameter b #(7 11))
(defparameter c #2A((7 11)
(13 17)))
(outer #'* a b)
;#2A((14 22)
; (21 33)
; (35 55))
(outer #'* c a)
;#3A(((14 21 35) (22 33 55))
; ((26 39 65) (34 51 85)))
Indexing operations
nested-loop
nested-loop is a simple macro which iterates over a set of indices
with a given range
(defparameter A #2A((1 2) (3 4)))
(aops:nested-loop (i j) (array-dimensions A)
(setf (aref A i j) (* 2 (aref A i j))))
A ; => #2A((2 4) (6 8))
(aops:nested-loop (i j) '(2 3)
(format t "(~a ~a) " i j)) ; => (0 0) (0 1) (0 2) (1 0) (1 1) (1 2)
sum-index
sum-index is a macro which uses a code walker to determine the
dimension sizes, summing over the given index or indices
(defparameter A #2A((1 2) (3 4)))
;; Trace
(aops:sum-index i (aref A i i)) ; => 5
;; Sum array
(aops:sum-index (i j) (aref A i j)) ; => 10
;; Sum array
(aops:sum-index i (row-major-aref A i)) ; => 10
The main use for sum-index is in combination with each-index.
each-index
each-index is a macro which creates an array and iterates over the
elements. Like sum-index it is given one or more index symbols, and
uses a code walker to find array dimensions.
(defparameter A #2A((1 2)
(3 4)))
(defparameter B #2A((5 6)
(7 8)))
;; Transpose
(aops:each-index (i j) (aref A j i)) ; => #2A((1 3)
; (2 4))
;; Sum columns
(aops:each-index i
(aops:sum-index j
(aref A j i))) ; => #(4 6)
;; Matrix-matrix multiply
(aops:each-index (i j)
(aops:sum-index k
(* (aref A i k) (aref B k j)))) ; => #2A((19 22)
; (43 50))
reduce-index
reduce-index is a more general version of sum-index; it
applies a reduction operation over one or more indices.
(defparameter A #2A((1 2)
(3 4)))
;; Sum all values in an array
(aops:reduce-index #'+ i (row-major-aref A i)) ; => 10
;; Maximum value in each row
(aops:each-index i
(aops:reduce-index #'max j
(aref A i j))) ; => #(2 4)
Reducing
Some reductions over array elements can be done using the Common Lisp
reduce function, together with aops:flatten, which returns a
displaced vector:
(defparameter a #2A((1 2)
(3 4)))
(reduce #'max (aops:flatten a)) ; => 4
argmax & argmin
argmax and argmin find the row-major-aref index where an
array value is maximum or minimum. They both return two values: the
first value is the index; the second is the array value at that index.
(defparameter a #(1 2 5 4 2))
(aops:argmax a) ; => 2 5
(aops:argmin a) ; => 0 1
vectorize-reduce
More complicated reductions can be done with vectorize-reduce,
for example the maximum absolute difference between arrays:
(defparameter a #2A((1 2)
(3 4)))
(defparameter b #2A((2 2)
(1 3)))
(aops:vectorize-reduce #'max (a b) (abs (- a b))) ; => 2
best
best compares two arrays according to a function and returns the ‘best’ value found. The function, FN must accept two inputs and return true/false. This function is applied to elements of ARRAY. The row-major-aref index is returned.
Example: The index of the maximum is
* (best #'> #(1 2 3 4))
3 ; row-major index
4 ; value
most
most finds the element of ARRAY that returns the value closest to positive infinity when FN is applied to the array value. Returns the row-major-aref index, and the winning value.
Example: The maximum of an array is:
(most #'identity #(1 2 3))
-> 2 (row-major index)
3 (value)
and the minimum of an array is:
(most #'- #(1 2 3))
0
-1
See also reduce-index above.
Scalar values
Library functions treat non-array objects as if they were equivalent to
0-dimensional arrays: for example, (aops:split array (rank array))
returns an array that effectively equivalent (eq) to array. Another
example is recycle:
(aops:recycle 4 :inner '(2 2)) ; => #2A((4 4)
; (4 4))
Stacking
You can stack compatible arrays by column or row. Metaphorically you can think of these operations as stacking blocks. For example stacking two row vectors yields a 2x2 array:
(stack-rows #(1 2) #(3 4))
;; #2A((1 2)
;; (3 4))
Like other functions, there are two versions: generalised stacking,
with rows and columns of type T and specialised versions where the
element-type is specified. The versions allowing you to specialise
the element type end in *.
The stack functions use object dimensions (as returned by dims to
determine how to use the object.
- when the object has 0 dimensions, fill a column with the element
- when the object has 1 dimension, use it as a column
- when the object has 2 dimensions, use it as a matrix
copy-row-major-block is a utility function in the stacking package
that does what it suggests; it copies elements from one array to
another. This function should be used to implement copying of
contiguous row-major blocks of elements.
rows
stack-rows-copy is the method used to implement the copying of objects in stack-row*, by copying the elements of source to destination, starting with the row index start-row in the latter. Elements are coerced to element-type.
stack-rows and stack-rows* stack objects row-wise into an array of the given element-type, coercing if necessary. Always return a simple array of rank 2. stack-rows always returns an array with elements of type T, stack-rows* coerces elements to the specified type.
columns
stack-cols-copy is a method used to implement the copying of objects in stack-col*, by copying the elements of source to destination, starting with the column index start-col in the latter. Elements are coerced to element-type.
stack-cols and stack-cols* stack objects column-wise into an array of the given element-type, coercing if necessary. Always return a simple array of rank 2. stack-cols always returns an array with elements of type T, stack-cols* coerces elements to the specified type.
arbitrary
stack and stack* stack array arguments along axis. element-type determines the element-type
of the result.
(defparameter *a1* #(0 1 2))
(defparameter *a2* #(3 5 7))
(aops:stack 0 *a1* *a2*) ; => #(0 1 2 3 5 7)
(aops:stack 1
(aops:reshape-col *a1*)
(aops:reshape-col *a2*)) ; => #2A((0 3)
; (1 5)
; (2 7))
Feedback
Was this page helpful?
Glad to hear it! Please tell us how we can improve.
Sorry to hear that. Please tell us how we can improve.